Toshiba patent calculates the final signal using the equation:
WDR=MAX(LS+SS×GA, SS×GA×R)
where LS and SS are samplings of the signals LPS and SPS, GA is a coefficient that may be equal to 1, and R=TL/TS is the ratio between the long integration TL and short integration TS times.
ST proposes not to reset floating diffusion node between the long and the short exposures. Together with the new signal calculation equation, this reduces the connection area non-linearity:
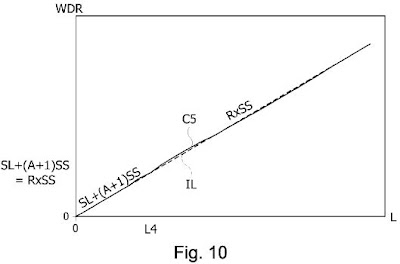
The proposed signal calculation equation is:
WDR=MAX(LS+SS+A×SS, R×SS)
where A is an optimization coefficient that may be equal to 0. The resulting improvement in linearity is shown on the graph:
The issue with 2 exposures is the drop in image quality at the switching point between short and long integration time. You want 40 dB range extension? Ok, here you get 20dB S/N drop...
ReplyDeleteAt the end of the day, it all boils down to how high the full well and how low the read noise your sensor has....you can always trade DR by SNR...no free lunch...
ReplyDeleteActually, ST's application examples are 2, 4, and 8 ratios between long and short exposures - quite modest DR extension. And SNR drop might be more acceptable too.
ReplyDeleteIndeed, the key of these kind DR extension is to be "reasonable". The more you increase the ratio, the more is your SNR droop. If you increase too much, you can even have missing codes in your reconstructed image! Ratio 8 is enough to unburn images with non visible added noise.
ReplyDeleteAnother interesting point using this DR principle is that you can optimize your CVF without sacrifying the Full Well. You'll get back exceed charges from your diode using the skimmed charges.